7 Modeling relatedness

The longitudinal model of the previous section uses pre-constructed correlations between observations that are close to each other in time in the fitting process.

A similar idea is used in modelling observations that have some inherent relationship on a continuous scale. A base structure of the variance-covariance matrix is created, and is then integrated in the fitting process (see ?sec-matc). There will be only one variance component to be estimated that is the scaling factor of the provided variance-covariance matrix structure.

Suppose the constructed distance matrix $G$ looks like this:

$G = [\begin{matrix} 1 & d_{a} & d_{b} & d_{c} & . & . & . & . \\ d_{a} & 1 & d_{g} & d_{h} & . & . & . & . \\ d_{b} & d_{g} & 1 & d_{k} & . & . & . & . \\ d_{c} & d_{h} & d_{k} & 1 & . & . & . & . \\ . & . & . & . & 1 & . & . & . \\ . & . & . & . & . & 1 & . & . \\ . & . & . & . & . & . & 1 & . \\ . & . & . & . & . & . & . & 1 \end{matrix}]$

with $d_{a}$ the (inverse) distance or relatedness between object 1 and 2, $d_{b}$ between object 1 and object 3, and so on. With the $d$ s between 0 and 1, with 1 being identical (no distance).

Remember that the classic grouped mixed model or single level hierarchical model can be represented like this:

$Y = X β + Z u + ε$ with X and Z are 0-1 incidence matrices (also called design matrices, respectively for fixed and random effects), $β$ are the to-be-estimated fixed effects coefficients, and $u$ the random effects following a multivariate normal $M V N (0, σ_{u}^{2} V)$ , and $ε$ the residuals following a normal distribution $N (0, σ^{2})$ .

Whereas the variance-covariance matrix $V$ in the grouped model is created for us via the software depending on which random effects we asked, is will now be of the form $σ_{r}^{2} G$ . Hence only variance component $σ_{r}$ needs to be estimated.

A common use case is where the $G$ matrix represents a relatedness matrix, where the genetic proximity, as defined by a pedigree or by calculation a distance matrix on the basis of genotype data. Yet the relatedness could be anything else (a physical distance, a similarity matrix between locations based on a multivariate environmental parameters,…)

To illustrate this principle we use the package lme4GS which is an extension of lme4.

The example is a breeding trial on a few hundred less or more related wheat lines. The data are obtained from the the package BGLR. The wheat data therein have a wheat.A matrix, which is a square symmetric matrix with in rows and columns the tested wheat lines, and carrying numbers between 0 (no relationship) and 2 (100% clones).

# to install lme4GS:
#devtools::install_git('https://github.com/perpdgo/lme4GS/',subdir='pkg_src/lme4GS')

library(lme4GS) 
data(wheat,package="BGLR")

wheat.A %>% as.vector() %>% hist(breaks=50)

The matrix wheat.Y contains the yields measured in a number of trials for each of the wheta lines. It requires some reformatting into a long data frame to allow it being processed by lme4GS.

wheat.Y.ldf <- wheat.Y %>% 
  as_tibble(rownames="genotype") %>% 
  rename_with(.fn=function(x) paste0("trial",x),.cols=(-genotype)) %>%
  pivot_longer(cols=starts_with("trial"),values_to="yield",names_to="trial")

The model without G (wheat.m1) and with G (wheat.m2) are fitted. In both cases genotype is a random effect, but in the latter extra refinement about the connection is provided.

wheat.m1 <- lme4::lmer(
  data = wheat.Y.ldf,
  yield ~ trial + (1|genotype)
)

wheat.m2 <- lme4GS::lmerUvcov(
  data = wheat.Y.ldf,
  yield ~ trial + (1|genotype),
  Uvcov=list(genotype=list(K=wheat.A))
)

Factoring method for matrix K associated with genotype was set to 'auto'

Computing relfac using Cholesky

iteration: 1
    x = 0.800380
    f(x) = 6713.109459
iteration: 2
    x = 1.400666
    f(x) = 7002.570832
iteration: 3
    x = 0.200095
    f(x) = 6628.125507
iteration: 4
    x = 0.250750
    f(x) = 6606.972653
iteration: 5
    x = 0.400821
    f(x) = 6588.152572
iteration: 6
    x = 0.404444
    f(x) = 6588.366062
iteration: 7
    x = 0.394818
    f(x) = 6587.858105
iteration: 8
    x = 0.388816
    f(x) = 6587.638853
iteration: 9
    x = 0.376810
    f(x) = 6587.432137
iteration: 10
    x = 0.374696
    f(x) = 6587.428453
iteration: 11
    x = 0.374096
    f(x) = 6587.429222
iteration: 12
    x = 0.374971
    f(x) = 6587.428370
iteration: 13
    x = 0.375031
    f(x) = 6587.428374
iteration: 14
    x = 0.374911
    f(x) = 6587.428374
iteration: 15
    x = 0.374970
    f(x) = 6587.428370

The random part of the summary output:

summary(wheat.m1)$varcor

 Groups   Name        Std.Dev.
 genotype (Intercept) 0.43277 
 Residual             0.90150

summary(wheat.m2)$varcor

 Groups   Name        Std.Dev.
 genotype (Intercept) 0.33658 
 Residual             0.89762

The genotype variance component is smaller in the second model but has a different meaning.

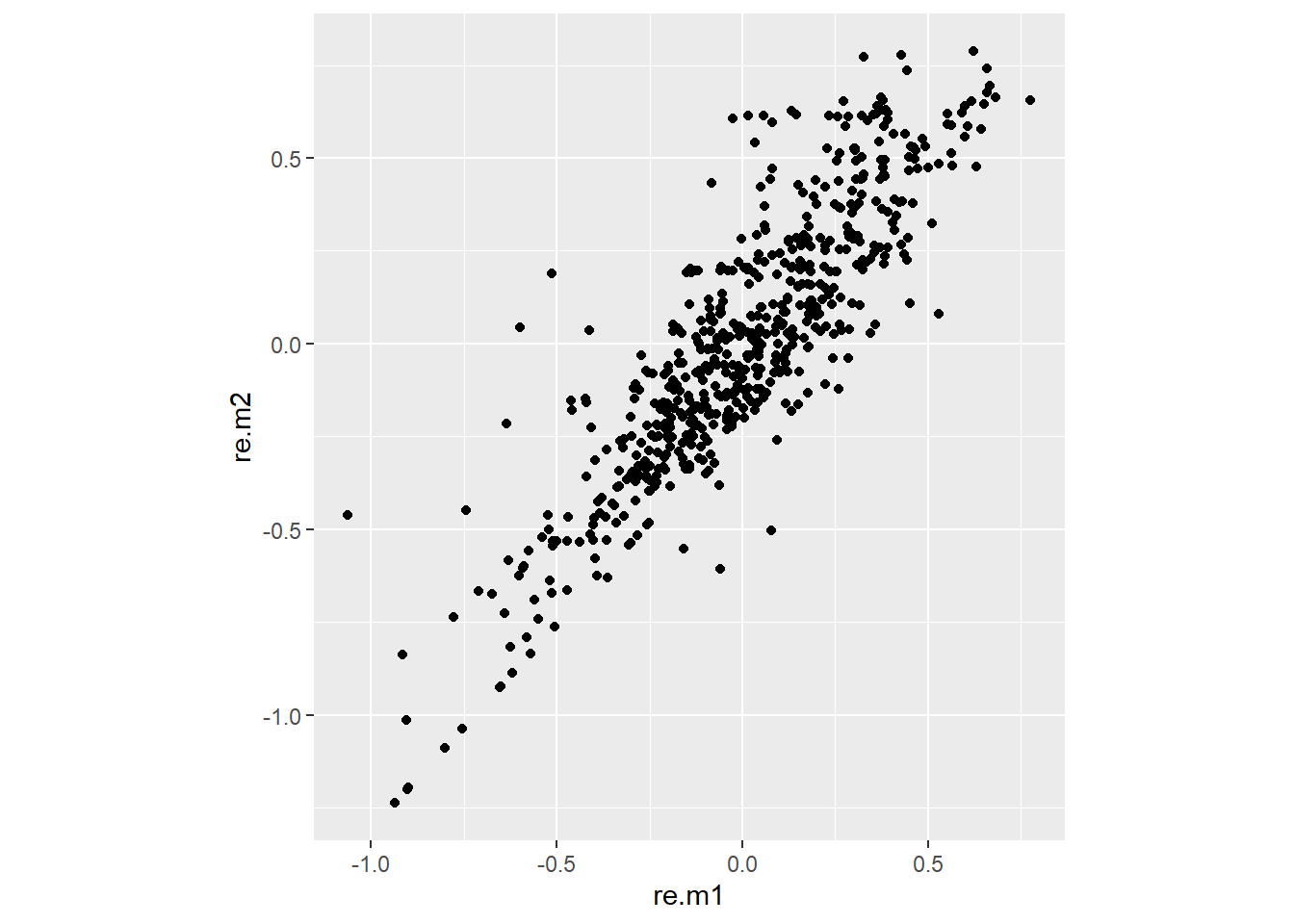
The biggest impact can be seen on the blups of the wheat lines in both models. (remark: due to a different parameterisation, the fixed intercept of wheat.m2 needs to be added to the blups of wheat.m2 )

KK <- data.frame(genotype=rownames(wheat.Y),
  re.m1=ranef(wheat.m1)$genotype[,1],
  re.m2=ranef(wheat.m2)$genotype[,1] + summary(wheat.m2)$coefficients[1,"Estimate"]
  )

KK %>% head()

  genotype      re.m1       re.m2
1      775 -0.6508369 -0.92288952
2     2166  0.2957093  0.35323191
3     2167 -0.9058979 -1.01421808
4     2465  0.5635522  0.58873260
5     3881 -0.1876134  0.05038266
6     3889  0.3835646  0.45027283

ggplot(KK,aes(y=re.m2,x=re.m1)) + 
  geom_point() + 
  coord_fixed()